4538. Bob and balls
Recently, Vasya
discovered that it is possible to play a very interesting game with balls. In
this game, balls are arranged in the form of various geometric figures and
solids. Currently, Vasya is arranging balls in the shape of an equilateral
triangle. However, there is a problem: sometimes he does not have enough balls,
and then he wants to know what is the maximum possible side length of such a
triangle given the number of balls he has.
Help Vasya: write
a program that computes n – the side length of the equilateral
triangle for a given number of balls k.
Below is an
example of arranging balls in the shape of an equilateral triangle:
Input. One positive integer k (0 ≤ k
≤ 2 *108) – the number of balls available.
Output. Print the
number n – the answer to the problem.
|
Sample
input |
Sample
output |
|
5 |
2 |
SOLUTION
combinatorics
Algorithm analysis
If n is the side
length of the triangle, then to completely fill it,
1 + 2 + … + n = n
* (n + 1) / 2
balls are required.
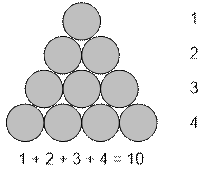
Suppose there are k balls
available. To find the maximum possible n, solve the equation
n * (n + 1) / 2 =
k
and round the non-negative
root down to the nearest integer.
Solve the quadratic
equation:
n2 + n – 2k = 0,
d = 1 + 8k, n = ![]()
The answer will be ![]() .
.
Algorithm implementation
Read the value of k.
scanf("%d",&k);
Compute and print the
answer.
n = int((-1 + sqrt(1.0 + 8*k)) / 2.0);
printf("%d\n",n);
Algorithm implementation – binary search
#include <stdio.h>
long long n, k, l, r, mid, res;
long long f(long long n)
{
return n * (n + 1) /
2;
}
int my_upper_bound(int start, int end, int x)
{
while (start <
end)
{
int mid = (start +
end) / 2;
if (f(mid) > x)
end = mid;
else
start = mid + 1;
}
return start;
}
int main()
{
scanf("%lld", &k);
// find min n: f(n) >= k
if (k == 0) res =
0;
else if (k == 1) res =
1;
else res =
my_upper_bound(0, k, k) - 1;
printf("%d\n", res);
}
Algorithm implementation – O(sqrt(n))
#include <stdio.h>
long long n, k, res;
long long f(long long n)
{
return n * (n + 1) /
2;
}
int main()
{
scanf("%lld", &k);
// find min n: f(n) >= k
n = 0;
while (f(n) <= k) n++;
printf("%d\n", n);
}